Automa a stati finiti

Gli automi a stati finiti sono uno dei concetti fondamentali nell'ambito dell'informatica, dell'ingegneria e della teoria dei sistemi. Questi dispositivi hanno un ruolo essenziale nell'elaborazione e nel controllo di informazioni in vari contesti, dalle applicazioni software alle macchine fisiche. In questa lezione, esploreremo cosa sono gli automi a stati finiti, come funzionano e dove vengono utilizzati.

Definizione di Automa a Stati Finiti

Un automa a stati finiti è un modello matematico di un sistema che può trovarsi in uno dei diversi stati finiti. Ogni stato rappresenta una condizione specifica del sistema, e il sistema può effettuare transizioni da uno stato all'altro in risposta a input o eventi esterni.

Componenti chiave di un Automa a Stati Finiti:

1. Insieme di Stati (Q): Gli stati rappresentano le condizioni in cui può trovarsi l'automa. Ogni stato è un elemento dell'insieme Q.

2. Insieme di Input (Σ): L'insieme Σ contiene tutti i possibili input o simboli che l'automa può ricevere.

3. Funzione di Transizione (δ): La funzione di transizione δ specifica come l'automa cambia stato in risposta a un input. È una mappa che associa una coppia (stato attuale, input) a uno stato successivo.

4. Stato Iniziale (q0): Questo è lo stato in cui si trova l'automa all'inizio dell'esecuzione.

5. Insieme di Stati Finali (F): Gli stati finali o accettanti sono gli stati in cui l'automa completa il suo processo e accetta l'input. F è un sottoinsieme di Q.

Funzionamento di un Automa a Stati Finiti

Il funzionamento di un automa a stati finiti è basato sul concetto di transizione di stato in risposta a input.

Iniziamo dallo stato iniziale (q0) e, a mano a mano che riceviamo input, seguiamo le transizioni definite dalla funzione di transizione δ. Continuiamo questo processo fino a quando raggiungiamo uno stato finale. Se alla fine dell'input ci troviamo in uno stato finale (che appartiene a F), l'automa accetta l'input; altrimenti, lo rifiuta.

Esempio semplificato Automa a Stati Finiti per un Semaforo

Immagina un automa a stati finiti per il controllo di un semaforo. In questo caso, ci sono tre stati principali:

1. Stato Rosso (q0): Iniziamo con il semaforo rosso, indicando che il traffico deve fermarsi. Questo è il nostro stato iniziale.

2. Stato Verde (q1): Quando riceviamo l'input "passaggio pedonale", transizioniamo dallo stato rosso al verde, consentendo il passaggio ai pedoni.

3. Stato Giallo (q2): Dopo un periodo di tempo prestabilito nel verde, transizioniamo dal verde al giallo per segnalare ai pedoni che il passaggio è in chiusura.

Quindi, il funzionamento di questo semaforo a stati finiti è abbastanza semplice. Iniziamo con il rosso, poi passiamo al verde quando riceviamo l'input "passaggio pedonale" e, infine, dopo un periodo di tempo, passiamo al giallo. Non appena il semaforo diventa giallo, potremmo considerare il passaggio a un altro input (come il ritorno al rosso) o farlo ciclare nuovamente verso il verde.

Questo esempio dimostra come gli automi a stati finiti possano essere utilizzati per modellare il comportamento di dispositivi comuni come i semafori, semplificando il controllo di sequenze di eventi.

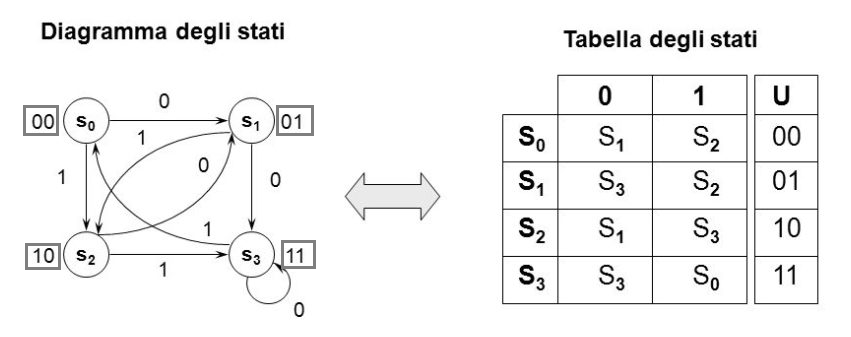
Ora disegna il "diagramma degli stati".

Applicazioni degli Automi a Stati Finiti

Gli automi a stati finiti hanno numerose applicazioni nel mondo reale, tra cui:

• Analisi sintattica di linguaggi di programmazione.
• Verifica di circuiti digitali e controllo di dispositivi.
• Riconoscimento di pattern in applicazioni di elaborazione di immagini.
• Analisi di reti e protocolli di comunicazione.

In sintesi, gli automi a stati finiti sono una parte fondamentale della teoria dei sistemi e dell'informatica, che ci aiutano a modellare e comprendere il comportamento di sistemi complessi. Sono uno strumento potente per risolvere una vasta gamma di problemi pratici attraverso l'automazione e il riconoscimento di pattern.